FUNCIONES LINEALES

Funciones lineales son aquellas que pasan por el origen de coordenadas, donde , de la forma: mientras que llaman función afín a la que tiene la forma: también conocida como transformación lineal, en el contexto de álgebra lineal.

Función lineal

La función lineal es del tipo:

Su gráfica es una línea recta que pasa por el origen de coordenadas.

Ejemplo

Para representar la función le damos al menos dos valores

Pendiente

 es la pendiente de la recta.

La pendiente es la inclinación de la recta con respecto al eje de abscisas.

Si 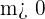 la función es creciente y el ángulo que forma la recta con la parte positiva del eje  es agudo.

Si  la función es decreciente y el ángulo que forma la recta con la parte positiva del eje  es obtuso.

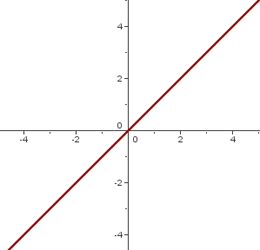
Función identidad

Su gráfica es la bisectriz del primer y tercer cuadrante.

Representar una función lineal en notación de funciones

Otro enfoque para representar funciones lineales es utilizar la notación de funciones. Un ejemplo de notación de funciones es una ecuación escrita en lo que se conoce como forma pendiente-intersección de una línea, donde x$x$ es el valor de entrada, m$m$ es la tasa de cambio y b$b$ es el valor inicial de la variable dependiente.

Forma de la ecuaciónNotación de la ecuacióny=mx+bf(x)=mx+b$$\begin{array}{ll}\text{Forma de la ecuación}\hfill & y=mx+b\hfill \\ \text{Notación de la ecuación}\hfill & f(x)=mx+b\hfill \end{array}$$

Como ejemplo utilizaremos un tren, podríamos utilizar la notación D(t)$D(t)$ en la que la distancia total D$D$ es una función del tiempo t.$t.$ La tasa, m,$m,$ es de 83 metros por segundo. El valor inicial de la variable dependiente b$b$ es la distancia original de la estación, 250 metros. Podemos escribir una ecuación generalizada para representar el movimiento del tren.

D(t)=83t+250$$D(t)=83t+250$$

Representar una función lineal en forma tabular

Un tercer método para representar una función lineal es mediante el uso de una tabla. La relación entre la distancia de la estación y el tiempo se representa en la Figura 2. En la tabla, podemos ver que la distancia cambia en 83 metros por cada aumento de 1 segundo en el tiempo.

Determinar si una función lineal es creciente, decreciente o constante

Las funciones lineales que hemos utilizado en los dos ejemplos anteriores aumentan con el tiempo, pero no todas lo hacen. La función lineal puede ser creciente, decreciente o constante. En el caso de una función creciente, como en el ejemplo del tren, los valores de salida aumentan a medida que aumentan los valores de entrada. El gráfico de la función creciente tiene una pendiente positiva. Una línea con pendiente positiva se inclina hacia arriba de izquierda a derecha como en Figura 5(a). En el caso de una función decreciente, la pendiente es negativa. Los valores de salida disminuyen a medida que aumentan los valores de entrada. Una línea con pendiente negativa se inclina hacia abajo de izquierda a derecha como en la Figura 5(b). Si la función es constante, los valores de salida son los mismos para todos los valores de entrada, por lo que la pendiente es cero. Una línea con pendiente cero es horizontal como en la Figura 5(c).

Figura 5

Funciones crecientes y decrecientes

La pendiente determina si la función es una función lineal creciente, una función lineal decreciente o una función constante.

• f(x)=mx+b es una función creciente si m>0,$f(x)=mx+b\text{ es una función creciente si }m>\mathrm{0,}$
• f(x)=mx+b es una función decreciente si m<0,$f(x)=mx+b\text{ es una función decreciente si }m<\mathrm{0,}$
• f(x)=mx+b es una función constante si m=0,